О задаче разложения числа в сумму
Рассмотрим следующую простую задачу.
Дан набор отрезков числовой оси, надо выбрать по одному числу из каждого отрезка таким образом, чтобы их сумма была равна заданному числу.
Дадим более формальную постановку.
Дано: 
Найти 
Задача легко решается, если догадаться сделать замену переменных:
Она позволяет перейти к более простой постановке:
Дано: 
Найти 
Сразу видно, что решение существует тогда и только тогда, когда 
Если мы быстро исчерпаем
Приведу код решения данной задачи на C++ (аж с ноября не публиковал здесь кода C++!).
#include <cassert>
#include <iterator>
#include <algorithm>
/**
* @brief Decompose a number into a sum of non-negative terms.
* @param value the value to be decomposed
* @param ubound non-negative upper bounds for decomposition terms
* @param decomp decomposition terms, of the same size as ubound!
* @return success (whether a decomposition exists)
*/
template
<
class NT, // number type
class NTArrayU, // number type array for ubound
class NTArrayD // number type array for decomp
>
bool scalar_sum_decompose
(
NT value,
NTArrayU const & ubound,
NTArrayD & decomp
)
{
if (value < NT{})
return false;
using std::size;
auto const n = size(ubound);
assert(n == size(decomp));
NT s {}; // accumulated sum.
for (auto i = n-n; i < n; ++i)
{
assert(!(ubound[i] < NT{}));
NT const term = std::min<NT>(value - s, ubound[i]);
decomp[i] = term;
value -= term;
}
return value == NT{};
}
(Код «auto i = n-n» есть маленький костыль ввиду нежелания городить извлечение типа размера.)
Теперь несложно написать и обёртку, решающую первую задачу.
#include <vector>
#include <numeric>
#include <functional>
/**
* @brief Decompose a number into a sum of bounded terms.
* @param value the value to be decomposed
* @param lbound lower bounds for decomposition terms
* @param ubound upper bounds for decomposition terms
* @param decomp decomposition terms, it must have the same size as ubound and lbound!
* @return success (whether a decomposition exists)
*/
template
<
class NT, // number type
class NTArrayL, // number type array for lbound
class NTArrayU, // number type array for ubound
class NTArrayD // number type array for decomp
>
bool scalar_sum_decompose
(
NT value,
NTArrayL const & lbound,
NTArrayU const & ubound,
NTArrayD & decomp
)
{
using std::size;
auto const n = size(ubound);
assert(size(lbound) == n && size(decomp) == n);
using std::begin;
using std::end;
std::transform(
begin(ubound), end(ubound), begin(lbound),
begin(decomp), std::minus<>{});
NT const lsum = std::accumulate(
begin(lbound), end(lbound), NT{});
std::vector<NT> buffer(n);
if (!scalar_sum_decompose(value - lsum, decomp, buffer))
return false;
std::transform(
begin(buffer), end(buffer), begin(lbound),
begin(decomp), std::plus<>{});
return true;
}
Вспомогательный буфер возник из-за запрета алиасинга итераторов в transform. Конечно, можно написать без transform и без буфера. И вообще одной функцией. Из-за вычисления сумм и разностей в плавающей точке теоретически могут возникнуть неприятности.
На пути к вычислению правильно округлённого значения гипотенузы
Пытаясь сделать вариант hypot(x, y), вычисляющий правильно округлённый результат для всех пар чисел x и y, я обнаружил, что используемая для проверки hypot_v3 может быть вовсе не так хороша, как я полагал.
В первой заметке я написал, что она обеспечивает погрешность <= 0.5 ULP, что неточно, так как происходит два округления: при вычислении корня в формате double и затем при конвертировании double во float. Технически погрешность <= 0.5 * (1 + DBL_EPSILON) ULP, эта маленькая добавка (DBL_EPSILON == 2.22045e-16) теоретически может сказаться в редких случаях.
Приведу некоторые очевидные свойства hypot(x, y):
1. Коммутативность: hypot(x, y) == hypot(y, x).
2. Чётность: hypot(-x, y) == hypot(x, -y) == hypot(x, y).
3. Округление: если |x| + |y| == max(|x|, |y|), то hypot(x, y) == max(|x|, |y|).
Данные свойства позволяют оценить количество "разных" пар x, y, дающих нетривиальный результат.
Всего имеется неотрицательных чисел float: 255·223 = 2139095040 (включая +бесконечность). Из них субнормальных 223-1 = 8388607 (с нулём), нормальных — 2130706433. Для субнормальных имеем 8388607·4194303 = 35184359505921 комбинаций. Для нормальных — 2130706433·224 = 35747322059030528 комбинаций. Всего 35782506418536449 ≈ 3.58e+16 комбинаций. Если считать, что DBL_EPSILON является хорошей оценкой вероятности ошибки, то умножив её на число комбинаций получим округлённо 8 — матожидание числа неверно округлённых пар. Считанные единицы, на которые можно надеяться натолкнуться только при переборе хотя бы одной восьмой всех возможных сочетаний значений x и y…
Увы, на практике всё несколько хуже. Для нормальных чисел. И много-много хуже для субнормальных! Действительно, оценка погрешности предполагает нормальную форму числа, при которой ULP имеет фиксированный (в относительной погрешности) вес (2-23). В субнормальных числах последняя цифра имеет больший вес вплоть до 100% (когда это единственная единица — в наименьшем представимом положительном числе). Исходя из этого наблюдения, можно попробовать добавить в hypot_v3 коррекцию порядка:
inline float hypot_v3a(float x, float y)
{
const double x_ = x, y_ = y,
s = x_ * x_ + y_ * y_;
if (s >= 0x1p-251)
return (float)std::sqrt(s);
return 0x1p-126f * (float)std::sqrt(0x1p+252 * s);
}
Эта небольшая поправка вроде бы вообще не должна влиять на цифры множителя, однако на практике резко уменьшает число дефектных результатов в субнормальной области (на момент написания я не наткнулся ни на одну подозрительную пару из субнормальных чисел). Среди нормальных подозрение вызывают, например, пары (0.0003162f, 1.661635309e-7f), (0.01f, 0.0001590774482f) и (1e+15f, 4.605317338e+15f).
Итак, я заменил проверочную hypot_v3 на hypot_v3a. Мы знаем, что результат sqrt(x*x + y*y) после коррекции порядка отличается от правильно округлённой гипотенузы не более, чем на вес последней цифры. Здесь надо сделать замечание по поводу того, что именно я под этим подразумеваю. Представление чисел в формате IEEE-754 обладает удобным свойством: их побитовым представлением можно оперировать как целым числом. В случае float 22 младших бита есть двоичные цифры множителя после запятой. Перед запятой подразумевается 1, если число нормальное, и 0, если субнормальное. За 22 битами цифр следует 8 бит порядка. Значение порядка 0 соответствует нулю и субнормальным числам. Значения 1—254 соответствуют нормальным числам (множители от 2-126 до 2127). Порядок 255 соответствует бесконечности (нулевые младшие 22 бита) и нечислам (ненулевые).
В моём случае получается, что модуль разности результата hypot_3a и результата вычисления корня одинарной точности, интерпретируемых как целые числа в соответствии с их двоичным представлением, не превосходит единицы. А значит, получив неточный результат z, я могу рассмотреть два соседних числа, добавив или вычтя 1 из двоичного представления z как из целого числа (то же, что std::nextafter(z, INFINITY), std::nextafter(z, 0.f), но стандартная реализация nextafter тоже не блещет скоростью — она предполагает обработку различных случаев, которых у меня не может быть). Итак, если удастся оценить погрешность результата, то помимо вычисленного значения должно быть достаточно проверить следующее (добавить единицу как к целому) и предыдущее (вычесть единицу как из целого) числа — какое-то из них может оказаться правильным ответом.
В начале, впрочем, я приведу улучшенную версию hypot_v2b, которая избегает работы с субнормальными числами.
inline float hypot_v2d(float x, float y)
{
x = std::fabs(x);
y = std::fabs(y);
float
min_ = x < y? x: y,
max_ = x < y? y: x,
mul, invmul;
if (max_ <= 0x1p-126f)
{
invmul = 0x1p-126f; // 0x1p-23 <= max_ <= 1
mul = 0x1p+126f; // 0x1p-23 <= min_ *
}
else if (max_ <= 0x1p-63f)
{
invmul = 0x1p-87f; // 0x1p-39 <= max_ <= 0x1p+24
mul = 0x1p+87f; // 0x1p-63 <= min_ *
}
else if (max_ <= 1.f)
{
invmul = 0x1p-24f; // 0x1p-39 <= max_ <= 0x1p+24
mul = 0x1p+24f; // 0x1p-63 <= min_ *
}
else if (max_ <= 0x1p+63f)
{
invmul = 0x1p+39f; // 0x1p-39 <= max_ <= 0x1p+24
mul = 0x1p-39f; // 0x1p-63 <= min_ *
}
else
{
invmul = 0x1p+102f; // 0x1p-38 <= max_ < 0x1p+26
mul = 0x1p-102f; // 0x1p-63 <= min_ *
}
max_ *= mul;
min_ *= mul;
if (max_ + min_ == max_)
return invmul * max_;
// * here.
return invmul * std::sqrt(max_* max_ + min_* min_);
}
Пусть есть два соседних числа в плавающей точке 
Заметим, что дискриминант обращается в нуль при 
Аналогично, выбрав 
Теперь воспользуемся double для того, чтобы написать «reference»-версию с оценкой погрешности на основе hypot_v2d.
namespace float_bits
{
using ifloat = std::int32_t;
using ufloat = std::uint32_t;
static_assert(sizeof(ufloat) == sizeof(float));
inline ufloat to_bits(const float x)
{
return reinterpret_cast<const ufloat&>(x);
}
inline float to_float(const ufloat bits)
{
return reinterpret_cast<const float&>(bits);
}
inline bool of_same_sign(float a, float b)
{
return ((to_bits(a) ^ to_bits(b)) >> 31) == 0;
}
inline float bits_prev(float x)
{
return to_float(to_bits(x) - 1);
}
inline float bits_next(float x)
{
return to_float(to_bits(x) + 1);
}
inline ufloat ulp_distance(float a, float b)
{
const auto x = to_bits(a), y = to_bits(b);
return x < y? y - x: x - y;
}
}
inline float hypot_v2e(float x, float y)
{
x = std::fabs(x);
y = std::fabs(y);
float
min_ = x < y? x: y,
max_ = x < y? y: x,
mul, invmul;
if (max_ <= 0x1p-126f)
{
invmul = 0x1p-126f; // 0x1p-23 <= max_ <= 1
mul = 0x1p+126f; // 0x1p-23 <= min_
}
else if (max_ <= 0x1p-63f)
{
invmul = 0x1p-87f; // 0x1p-39 <= max_ <= 0x1p+24
mul = 0x1p+87f; // 0x1p-63 <= min_
}
else if (max_ <= 1.f)
{
invmul = 0x1p-24f; // 0x1p-39 <= max_ <= 0x1p+24
mul = 0x1p+24f; // 0x1p-63 <= min_
}
else if (max_ <= 0x1p+63f)
{
invmul = 0x1p+39f; // 0x1p-39 <= max_ <= 0x1p+24
mul = 0x1p-39f; // 0x1p-63 <= min_
}
else
{
invmul = 0x1p+102f; // 0x1p-38 <= max_ < 0x1p+26
mul = 0x1p-102f; // 0x1p-63 <= min_
}
max_ *= mul;
min_ *= mul;
if (max_ + min_ == max_)
return invmul * max_;
const double a = max_, b = min_, s = a*a + b*b;
const float
s_ = (float)s,
s0 = std::sqrt(s_),
s1 = float_bits::bits_prev(s0),
s2 = float_bits::bits_next(s0);
const double d0 = s0, d1 = s1, d2 = s2,
q0 = s - d0 * d0,
q1 = s - d1 * d1,
q2 = s - d2 * d2,
aq1 = std::fabs(q1),
aq2 = std::fabs(q2);
float res = s0;
if (aq1 < aq2)
{
const auto q1_0 = d1 - d0,
d = 2. * (q1 + q0) + q1_0 * q1_0;
if (d < 0. ||
(d == 0. && (float_bits::to_bits(s1) & 1) == 0))
res = s1;
}
else if (aq2 < aq1)
{
const auto q2_0 = d2 - d0,
d = 2. * (q2 + q0) + q2_0 * q2_0;
if (d > 0. ||
(d == 0. && (float_bits::to_bits(s2) & 1) == 0))
res = s2;
}
return invmul * res;
}
Результат hypot_v2e совпадает с результатом hypot_v3a почти везде: проверялись все x из набора { 3.16227766e-4f, 0.f, 1e-40f, 0x1p-126f — 0x1p-127f, 0x1p-126f, 1e-30f, 1e-20f, 1e-15f, 1e-6f, 1e-2f, 1.f, 1e+2f, 1e+6f, 1e+15f, 1e+20f, 1e+30f } для всех неотрицательных представимых чисел y — было найдено всего четыре пары (x, y), для которых результаты не совпали — три из них были приведены выше как «подозрительные».
Я написал аналог hypot_v2e, который оперирует только значениями float. Точное возведение в квадрат выполняется с помощью разрезания множителя числа на две 12-битные половинки (hi и lo). Затем вычисляются слагаемые hi*hi, lo*lo и 2*hi*lo. Результат — суммарно 50 отличающихся от hypot_v3a результатов (для того же перебора x-y), т.е. в среднем 1 ошибка на несколько сот миллионов пар (x, y). Тем не менее, не скажу, что такой результат мне особенно понравился. Хотелось бы почти полного совпадения с hypot_v2e или большей простоты кода…
Эксперименты с hypot III
В посте Эксперименты с hypot я допустил существенную неточность: указал ссылку на реализацию std::hypot (double) без проверки реализации std::hypotf (float), в то время как для сравнения использовалась как раз версия одинарной точности. Итак, hypotf.
Оказывается, это, по сути, та же hypot_v3! Я было думал, что hypotf использует ту же методику, что и hypot. В этой мысли меня поддерживало и её низкое быстродействие (в 5 раз медленнее hypot_v3). Видимо, дополнительные проверки оказались столь дороги. Таким образом, с одной стороны, очевидно, что результаты hypot_v3 и hypotf (для чисел) совпадут. С другой стороны, разработчики руководствовались теми же соображениями, что и я. Функция hypot_v3 даёт корректно округлённый результат в одинарной точности, и её можно использовать для экспериментальной проверки прочих вариантов.
Вариант в двойной точности не мог быть создан с помощью того же приёма, так как четверная точность не поддерживается аппаратно на большинстве процессоров, а программная реализация очень медленная и требует подключения специальной библиотеки (хотя она и есть в комплекте gcc). И вот тут возник вопрос: float vs double даёт возможность проверить качество того или иного алгоритма, а если мы его применяем только в double, то мы, по сути, ограничены теоретическим анализом.
Я, наконец, прочёл комментарий в e_hypot.c, который, вроде бы (с кодом не сравнивал), описывает применённый там метод. А метод основан на соображении следующего вида:
«If (assume round-to-nearest) z=x*x+y*y has error less than sqrt(2)/2 ulp, than sqrt(z) has error less than 1 ulp (exercise).»
Т.е. если вычислить правильно округлённую сумму квадратов, то и корень будет правильно округлён (докажите, ага). Конечно, чисто формально можно разложить в ряд:
Если привести абсолютную погрешность к относительной, то получим
В первом приближении извлечение корня уполовинивает относительную погрешность! С такой точки зрения, у нас должен получаться правильно округлённый результат даже в том случае, если последняя цифра z неверна. Впрочем, следует учесть погрешность вычисления самого корня. Если считать, что эпсилон = 0.5 ULP, то у нас появляется дополнительная относительная погрешность 
Т.е. всё же ошибка в 0.75 ULP. Я выше написал «правильно округлён», но это, увы, не то же самое, что «ошибка меньше 1 ULP». Ошибку меньше 1 ULP мы получили, но для «правильно округлён» требуется ошибка не более 0.5 ULP, чего мы не достигаем. Эксперимент показывает, что, действительно, вычисление вида
float hypot_v2c(float x, float y)
{
x = std::fabs(x);
y = std::fabs(y);
float
min_ = x < y? x: y,
max_ = x < y? y: x,
mul, invmul;
if (max_ + min_ == max_)
return max_;
// max_ != 0
// min_ >= 0x1p-24 * max_
if (max_ <= 0x1p-126f)
{
invmul = 0x1p-126f; // 0x1p-23 <= max_ <= 1
mul = 0x1p+126f; // 0x1p-23 <= min_
}
else if (max_ <= 0x1p-63f)
{
invmul = 0x1p-63f; // 0x1p-63 <= max_ <= 1
mul = 0x1p+63f; // 0x1p-87 <= min_
}
else if (max_ <= 1.f)
{
invmul = 1.f; // 0x1p-63 <= max_ <= 1
mul = 1.f; // 0x1p-87 <= min_
}
else if (max_ <= 0x1p+63f)
{
invmul = 0x1p+63f; // 0x1p-63 <= max_ <= 1
mul = 0x1p-63f; // 0x1p-87 <= min_
}
else
{
invmul = 0x1p+127f; // 0x1p-64 <= max_ < 2
mul = 0x1p-127f; // 0x1p-88 <= min_
}
max_ *= mul;
min_ *= mul;
const double a = max_, b = min_, s = a*a + b*b;
return invmul * std::sqrt((float)s);
}
даёт ошибку в последней двоичной цифре, хотя и немного реже, чем вариант hypot_v2b. Следовательно, то же поведение можно ожидать от std::hypot: ошибка в последней цифре. Т.е. она немногим лучше прямого вычисления в духе hypot_v2b. В связи с этим возникает вопрос: можно ли более-менее эффективно вычислить действительно правильно округлённую гипотенузу, не прибегая к арифметике удвоенной разрядности. И ещё: как быть с длиной n-мерного вектора? Метод hypot_v2b можно применить к n-мерному вектору: найти максимум по абсолютной величине, выбрать порядок, вычислить сумму промасштабированных квадратов с компенсацией и потом уже взять корень, и можно надеяться на погрешность в одну-две последних цифры.
Аналитическое обращение матриц из одного узкого класса
Disclaimer: вполне вероятно, что данный результат давно был кем-то получен или выводится из каких-то более общих результатов для матриц подобного вида, но я не знаток матричной математики, а серьёзный поиск предпринимать было лень.
Пусть n ∈ ℕ, определим A(n) как n×n-матрицу следующего вида:
1 2 3 ... (n−2) (n−1) n
2 3 4 ... (n−1) n 1
3 4 5 ... n 1 2
...
...
...
(n−2) (n−1) n ... (n−5) (n−4) (n−3)
(n−1) n 1 ... (n−4) (n−3) (n−2)
n 1 2 ... (n−3) (n−2) (n−1)
Википедия сообщает, что данные матрицы являются подмножеством класса матриц, называемых «антициркулянтами».
Оказалось, что для любого n не составляет труда выписать матрицу A−1(n). Приведённая ниже конструкция была получена эмпирически, затем проверена аналитически «на бумажке».
Обозначим q = 1 + 2 + … + n = n(n + 1)/2, a = (1 − q), b = (1 + q), c = nq, тогда матрица cA−1(n) имеет следующий вид:
a 1 1 1 ... 1 b 1 1 1 ... 1 b a 1 1 ... 1 b a 1 ... ... ... 1 1 b a 1 ... 1 1 b a 1 1 ... 1 b a 1 1 1 ... 1
То есть также является «антициркулянтом», не содержащим нулевых элементов.
Доказать то, что указанная конструкция действительно даёт нам обратную к A(n) матрицу, не составляет большого труда. Для этого достаточно проверить, что:
- (1, 2, 3, …, n)T(a, 1, 1, …, 1, b) = c;
- при i = 1, 2, …, (n−1) имеем i(b + a) + a + q − 2i − 1 = 0 — для всех прочих перестановок.
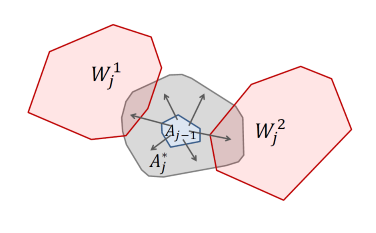
Алгоритм построения траектории при наличии фазовых ограничений II
Трубка внутри множества достижимости в обход препятствий
Подчищенная и сокращённая версия (март 2015) предыдущего варианта.
К тому моменту я сделал тестовую реализацию алгоритма в двумерном пространстве (с визуализацией в 3D). К сожалению, запустить её на конференции не получилось, так как оказалось, что на Windows XP SP3 exe, скомпилированные Visual Studio 2013, не запускаются. На случай подобных проблем у меня, естественно, были заготовлены скриншоты:
Perfect Hashing of Very Short Strings
This post is a (bit modified) translation of my older post in Russian.
Let a small set of very short strings (1—4 bytes here) is given and we want to construct a dictionary with strings from this set being used as keys. A simple solution is to use a universal hash table with a generic hash function (usually the one provided by the library implementing the hash table, e.g. C++ Standard library provides some std::hash implementation for strings) such as Murmur or FNV hashes.
However such a solution is a heavyweight one in some cases, for example when keys are known in advance and are short enough. This is the case when a generic array may handle the job. For this to be true we have to find a hash function that suffers no collisions for inputs from the set of our keys, so called perfect hash function.
Another feature I want is high hash computation speed, so I am not going to use complex and costly hash functions. For example Pearson hashing is too complex for me (plus I am considering CPUs capable of fast integer hardware multiplication). Finally, I am not going to use division or remainder operations. Instead I will use an array having size equal to some power of 2 (I am OK with some cells left unused).
For strings no longer than four bytes I can use 32-bit words as keys, «NUL» character is not used in texts so one-character strings have only the least significant byte being non-zero and the other three bytes being zero, two-character strings have the least significant half non-zero and the other half zero and so on. The function casting strings to integers that way may be written in C++ as follows.
inline uint32_t to_number(const std::string &word)
{
register uint32_t result = 0;
switch (word.size())
{
case 4: result = (uint32_t)word[3] << 24;
case 3: result |= (uint32_t)word[2] << 16;
case 2: result |= (uint32_t)word[1] << 8;
case 1: result |= word[0];
default: return result;
}
}
The hash function I am going to construct belongs to the family defined by the following template (one has to find N and b for the given set of keys).
template <uint32_t N, unsigned b>
uint32_t ssphash(uint32_t word)
{
return (word * N) >> b;
}
Of course, there is no guarantee that for the given set of keys this family of functions contains a perfect hash function. But due to its simplicity and small combinatorial size of the problem (for modern computers) we can try to brute-force N and b (the software was written for MSVC and uses _alloca from malloc.h and intrinsic __lzcnt from intrin.h, some CPUs do not support the latter). The size of the array (our hash table) is taken as the smallest power of 2 not less than quantity of keys.
For examples for the following set of keys (operator and punctuation lexemes of C++)
+ - ! ~ # % ^ & * ( ) / // /* */ [ ] { } | ? : ; , . && || ++ -- < > " ' <= >= = == -> .* ->* << >>
I have got N == 242653, b == 17.
Xor delta coding
This post is a (bit modified) translation of my older post in Russian.
Delta coding is widely used as a component of different algorithms e. g. data compression or digital signal processing. Delta encoding is done through computation of differences between adjacent elements of a sequence and hence is the result of applying the first-order finite difference operator, which is a discrete analogue of a continuous differential operator. Delta decoding is done through computation of partial sums and is a discrete analogue of a continuous integration operator.
Delta encoding has the following important feature: a sequence of repeating values produces a sequence of zeroes. That made me ponder what if difference be replaced with something else conserving the mentioned property of converting sequences of repeating values into zeroes. The obvious candidate (for the case when values have fixed-size binary representation) is the bitwise exclusive or operation (xor; do other viable candidates exist?). This operation is commutative and associative. It also has the following properties (for any a):
- a xor 0 ≡ a;
- a xor a ≡ 0.
A corollary of this is (a xor b) xor b ≡ a for any a and any b. (This is the base of the well-known trick of swapping values of two variables without explicitly using temporary storage.)
Thus for a set of functions defined as { xora | a ∈ Z, xora(x) ≡ a xor x } we have an identity element xor0. Any element of this abelian group (with function composition operation) is an inverse to itself.
These properties made xor popular in cryptographic algorithms (is there any well-known cipher or hash that doesn’t use it?).
The following code replaces addition and subtraction in «classic» delta coding algorithm with bitwise xor.
void xor_delta_encode(char *begin, size_t n)
{
char prev = begin[0], t;
for (size_t i = 1; i < n; ++i)
{
t = begin[i];
begin[i] ^= prev;
prev = t;
}
}
void xor_delta_decode(char *begin, size_t n)
{
char prev = begin[0];
for (size_t i = 1; i < n; ++i)
prev = begin[i] ^= prev;
}
Simple testing code is available here.
This code has an amusing property: repeated xor-delta encoding leads to coincidence of prefixes of the resulting sequence and the original sequence. It can be shown on paper (due to properties of xor) that after 2n repeats we have coincidence of prefix of length 2n (or coincidence of the entire sequences if the original sequence is no longer than 2n). Therefore after 2N repeats of encoding, where N = ceil(log2(sequence length)), we have the original sequence recovered. Repeating of the inverse operation (decoding) has the same property and enumerates the same intermediate sequences but in inverse order.
Алгоритм построения траектории при наличии фазовых ограничений
Презентация по разработанному в этом году геометрическому алгоритму построения приближённой траектории линейной управляемой системы с выпуклым множеством управления и фазовыми ограничениями, заданными в виде наборов выпуклых многогранников. Алгоритм основан на двоичных разбиениях пространства (BSP).
Ссылка на презентацию
Совершенное хэширование сверхкоротких строк
Пусть заранее задан небольшой набор сверхкоротких строк и надо сделать словарь, ключами которого могут быть эти строки. Обычным решением для произвольных строк является использование универсальной хэш-таблицы с достаточно универсальной хэш-функцией (например, Murmur или FNV) из той или иной библиотеки (например, std::unordered_map).
Однако, данное решение является очень тяжеловесным, если строки-ключи заведомо очень короткие (далее я ориентируюсь на строки не длиннее четырёх байт), и, главное, известны заранее. В такой ситуации представляется разумным хранить ассоциированные значения в обычном массиве и подобрать такой хэш, который именно на данном заранее известном наборе не даёт коллизий, — совершенный хэш.
Я хочу чего-то с очень высоким потенциальным быстродействием, поэтому я не буду использовать вычислительно дорогие хэш-функции. Например, функция Пирсона слишком тяжеловесна для моего случая (при том, что я ориентируюсь на процессоры, способные быстро умножать). Я также не буду использовать операцию взятия остатка от деления, поэтому мой массив будет размера равного степени двойки.
Сверхкороткие строки можно хранить в одном машинном слове. Четыре байта — 32-битное целое. Пусть, при этом, строки единичной длины соответствуют ненулевому младшему байту (три остальных — нули), строки длины два — двум младшим ненулевым байтам (два остальных — нули) и так далее. Функция приведения строки к числу такого вида может быть записана следующим образом:
inline uint32_t to_number(const std::string &word)
{
register uint32_t result = 0;
switch (word.size())
{
case 4: result = (uint32_t)word[3] << 24;
case 3: result |= (uint32_t)word[2] << 16;
case 2: result |= (uint32_t)word[1] << 8;
case 1: result |= word[0];
default: return result;
}
}
Хэш будем искать вида
template <uint32_t N, unsigned b>
uint32_t ssphash(uint32_t word)
{
return (word * N) >> b;
}
Конечно, нет никакой гарантии, что совершенный хэш такого вида для заданного набора строк существует. Но мы можем попробовать подобрать нужные N и b прямым перебором. Для чего я написал программу, которую можно взять здесь.
Данная программа позволяет ввести набор строк и перебором ищет подходящие N и b. Размер хэш-таблицы выбирается как степень двойки не меньшая числа строк-ключей. Например, для лексем (операторы и пунктуация) C++
+ - ! ~ # % ^ & * ( ) / // /* */ [ ] { } | ? : ; , . && || ++ -- < > " ' <= >= = == -> .* ->* << >>
получены значения N == 242653, b == 17.
Xor-Δ-кодирование
Дельта-кодирование является распространённым составным элементом различных алгоритмов сжатия данных и обработки дискретных сигналов. Дельта-кодирование выполняется путём вычисления разностей между соседними элементами последовательности (и напоминает дифференцирование). Дельта-декодирование выполняется путём накапливания частичных сумм (и напоминает, соответственно, интегрирование).
Одним из характерных свойств дельта-кодирования является то, что последовательность повторяющихся значений кодируется последовательностью нулей. В связи с этим, мне стало интересно, что получится, если заменить и вычитание и сложение одной операцией — вычислением поразрядного исключающего или (xor). Данная операция коммутативна и ассоциативна. Кроме того, она обладает следующими двумя свойствами (для любого числа a):
- a xor 0 ≡ a;
- a xor a ≡ 0.
Откуда легко выводится тождество (a xor b) xor b ≡ a.
Таким образом, если мы определим множество функций { xora | a ∈ Z, xora(x) ≡ a xor x }, то единица этого множества — тождественное преобразование xor0, и каждый элемент этого множества является обратным к самому себе относительно операции композиции функций (в частности, множество таких функций является абелевой группой относительно операции композиции).
Благодаря своим свойствам, операция xor очень популярна в области криптографических алгоритмов.
Итак, я написал следующий C++-код, заменяющий операции вычитания и сложения в дельта-кодировании/декодировании на операцию поразрядного исключающего или.
void xor_delta_encode(char *begin, size_t n)
{
char prev = begin[0], t;
for (size_t i = 1; i < n; ++i)
{
t = begin[i];
begin[i] ^= prev;
prev = t;
}
}
void xor_delta_decode(char *begin, size_t n)
{
char prev = begin[0];
for (size_t i = 1; i < n; ++i)
prev = begin[i] ^= prev;
}
Тестировочный код целиком: Bitbucket.
Если запустить этот код, то можно увидеть довольно забавное свойство (которое и сподвигло меня написать этот пост).
Повторное xor-дельта-кодирование приводит к повторению префиксов исходной последовательности. А именно (это можно показать «на бумажке», сокращая элементы благодаря свойствам операции xor): после 2n повторений имеем совпадение с исходной последовательностью префикса длины до 2n. Через 2N повторений операции кодирования, где N = ceil(log2(длина последовательности)), имеем восстановление исходной последовательности, «круг замкнулся». Повторение обратной операции (xor-дельта-декодирования) перебирает те же 2N возможных последовательностей, но уже в обратном порядке.
evetro 